クロールは游脚が１足なので、４足が順に游脚となって１サイクルの歩容となる。つまり、各足が游脚となるタイミングは１サイクルの１/４となる。これを図にすると右図の様になる。第１～第４足にそれぞれどの足が当てはまるかという問題はまだ残っているが、これで常に３本の足で接地している状態となる。クロール歩行の分析と合成
2003.4.29
歩行には色々な形態がある。アイボは四肢に３自由度を持ったロボットであるが、各足に足首が無いため、2足状態でバランスを取ることが不可能である。このため、４足のうち同時に２足が游脚となる歩容は取ることができない。アイボの基本的な歩容は「クロール」歩容という事になる。
クロール歩容
クロール歩容は４足のうち３足を順に後に送る事で進む歩行形態で、静歩行が可能である。OPEN-R SDKのサンプルプログラムでは「MoNet」でクロール歩容のモーションが提供されている。
クロール歩容の分析
歩行する際の足の動きはどのような歩容でも同じである。すなわち、接地している状態で足を後に送って体全体を前に送り、他の足で体を支えた状態で足を浮かせて前に戻す。これを複数の足で協調しながら連続動作することで歩行を実現する。歩容によりこのタイミングが異なる。
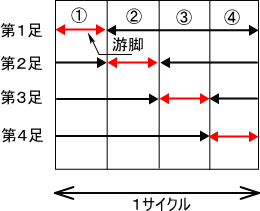
クロールは游脚が１足なので、４足が順に游脚となって１サイクルの歩容となる。つまり、各足が游脚となるタイミングは１サイクルの１/４となる。これを図にすると右図の様になる。第１～第４足にそれぞれどの足が当てはまるかという問題はまだ残っているが、これで常に３本の足で接地している状態となる。
足の動きと動きの速度
アイボの足（前足）の動きを図に示す。図中の①から④はタイミング図の①から④に対応する。このように時間にすると游脚である期間は接地脚である期間の１/３であるが、移動距離は軌跡の長さとなるので地面から浮かせる分だけ接地脚期間より長い。よって動きの速度は3倍以上となる。
３足立ちと重心
クロール歩行を行なっている間はほぼ全期間に渡って３本足で立たなければならない。アイボの重心を点とすると重心点が接地足３本を結んで作られる三角形の中に入っていれば３本足で立つ事ができることになる。アイボの体重のほとんどは胴体と頭部で占められている。前足より前に頭がついていることから重心点は胴体中心より少し手前にあると考えられる。更に、重量の分布範囲が広いことから重心点だけで考えることはできない。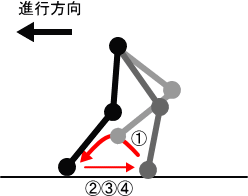
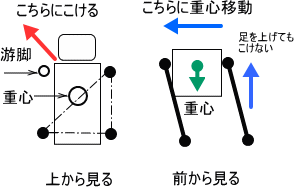つまり、３本足で立つ場合には重心を十分に３本足の接地点でできる安定域に納めるように重心を移動させる必要がある。具体的には四肢をX方向（横方向）に同期移動させることで重心を游脚とならない側に移動させる。
ここで今までの内容を整理してみる。
①４足のうちの３足が常に接地しており、同じ速度で後ろに送り出すことで体を前に送り出す。
②足を前に戻す動作は１足ずつ行なう。前に戻す速度は後ろに送り出す速度の３倍以上
③足を前に戻す動作を行なう際には、重心をその足の反対側に移動させる必要がある。そのために４足を協調してこれから前に戻す足側に移動させる。
次にこれらの一連の動作を連続して行なうことを考える。
左右の往復動作と游脚タイミング
左右２足ずつの足を動かし、游脚とする時には胴体を左右のいずれか（游脚の逆方向）に移動させるのであるから、連続動作として考える時、胴体を左右に揺さぶり、その適度なタイミングで４本の足を游脚として当てはめるのがよさそうである。
胴体の揺さぶりに游脚を当て嵌める組み合わせはいくつかあるが、自然界の動きから最も効率がよさそうな、胴体を左→右（右→左でもよいが）と揺さぶる動作を１周期とし、これに４本の游脚を当て嵌める動作を考える。
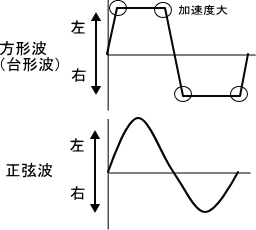
胴体を揺さぶる動きをどのようにするかを考える。静歩行で考えるとアイボの重心を完全に接地足に移してから游脚を上げることになるので特に考えることは無い。ただ、加速度は予測外の動作を引き起こすため、低速での動作となる。ここでは生活レベルでの歩行を考えるため、準動歩行とし、加速度による重心移動（静的には重心は移動していないが加速度があるため、転倒しない状態）を狙った動きとしたい。そのためには左右に勢い良く揺さぶる方形波（またはそれに近い台形波）が考えられるが、加速度が強すぎると制御しづらいし、現段階では加速度での動作をフィードバックする制御は考えていないため、制御不能となる可能性が高い。そこで重心の移行加速はある程度期待できるが、過度の加速度を与えない正弦波（サイン波）での動作とする。
次に往復動作に游脚を当て嵌めてみる。図の様に胴体を左→右と揺さぶる１周期動作に游脚を当て嵌めると、体の位置と游脚は左右逆の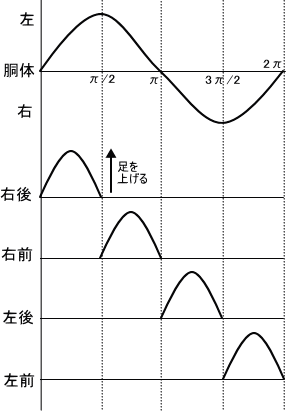
関係なので右足・右足・左足・左足の準に游脚とすればよいことになる。もう少し詳細に書くと、左に体をゆすり初めてから最も左に体が移動するまで（位相で言うと０～π/２）に右前足か右後足を游脚とし、最も左から中心まで（位相でいうとπ/２～π）の間に右のもう片方の足を游脚とする。次いで体が右に移動するタイミング（位相ではπ～２π/３・２π/３～２π）で左前足・左後足を游脚にする。
「行き」（０～π/２）に前足を当て嵌めるのが良いか「帰り」（２/π～π）に前足を当て嵌めるのが良いかの考察であるが、「行き」は中心地点（位相ゼロ）からの開始となるため、重心が中央付近にある。対して「帰り」は最も左の状態（位相２/π）から開始するため、重心はしっかりと片側に移っている。そのため、頭部の重量がかかっている前足を游脚とするのは「帰り」が良いようである。「行き」の開始時点では重心が中央にあるため、足を上げた瞬間にバランスを崩す恐れがあるのだが、実際には加速度があるため静止状態での重心位置で考えるより安定している。正弦波の加速度は正弦波の微分である余弦波（コサイン波）で与えられるので「行き」の開始時点は加速度が最高、「帰り」の開始時点では加速度は最低となる。
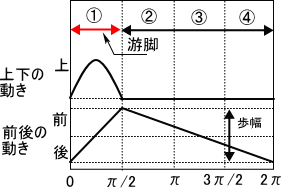最後に四肢の前後の動きを考える。四肢が位相π/２ずつずれて動いているため接地脚の移動速度は一定である必要がある。游脚となっている期間の前後の動きは接地脚時のちょうど３倍となるため、左図のような動きとなる。
上下の動きは特に制限や理論は無いが、正弦波の０～πの曲線を用いるのがよいのではないかと思う。
動作の実装
以上の内容をプログラムとして実装する。特に難しいことはないので詳細の説明は省略するが、要点のみ上げる。
動きの関数
周波数と時間から位相を計算する。
ただし、θは0～2πの剰余数とする。
左右の動き
前後の動き
上下の動き
歩行準備動作
直立状態から歩行を開始するには直立から歩行への移行動作が必要となる。直立状態から歩行モーションのあるフレームに移行するモーションを実行することで歩行姿勢へ移行することが考えられる。これは歩行と同様に１周期の動作中に現状姿勢（直立姿勢）から位相ゼロの時の、四肢の前後方向足位置へ移動させるモーションを生成させることで移行させることができる。実際には前後方向のオフセット・左右方向のオフセット・高さなどの要素がある他、歩行パラメータが変わった場合等を考慮しX・Y・Z全ての要素において移行を行なう必要がある。
進行方向
ここでは前進を前提に考えたが、Y方向の極性を反転することで後退することができる。
方向変換
ここでは直進を前提に考えたが、地面平面の任意点を中心とする円弧上を進むように考えることで直進・カーブ・その場回転・横歩きなどのモーションを生成することができる。
以上
