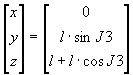
IKベースのモーション再生プログラム

2003.4.27

アイボは四肢に３自由度の関節を持つロボットである。アイボの関節を制御するには各関節の角度を適度に移動させることによるが、思い通りの動きをさせるにはその角度・移動速度など多くの計算を必要とする。

歩くことを前提に考えると四肢の先端（肉球部）はほぼ常に接地しており（游脚は浮いているが）足の付け根から肉球部までの位置関係を角度に変換できる式を用意すれば計算が簡単になる。ここで、ある関節角度の時に足先端がどの位置になるかの計算を「順運動計算」、足先端がある位置にあるときの関節角度を計算することを「逆運動計算」（インバース・キネマティクス）という。

アイボの構造と物理的定数

アイボの場合、可変要素は「肩」・「脇」・「膝」の３ヶ所の関節角度であり、肩から膝、膝から先端の長さは変わらない定数となる。ここでは肩から膝、膝から肉球までの長さが同じとして計算を簡略化している。

順運動計算

アイボの足構造での順運動計算をまとめる。

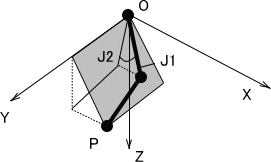
アイボは肩関節（J1）に脇関節(J2)が付き、その先端に膝関節（J3)が付いた構造になっている。これより、
J1・J2をゼロとおくと、

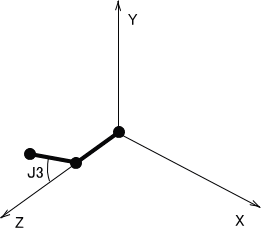
となり、J2を加えると、Y軸を軸に回転するので回転行列を左からかけて、

となる。

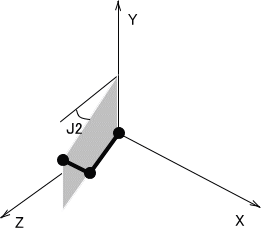
J1を加えると、X軸を軸に回転するのだが、アイボのJ1関節の回転方向はXYZ座標と極性が逆となるため -J1とおく。

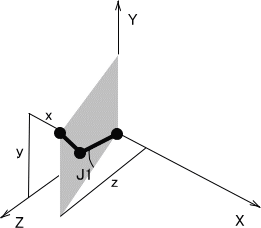
以上で簡易的ではあるが関節角度（J1，Ｊ2，J3)から肉球部座標を求められる。

逆運動計算

逆に肉球部座標から各関節角度を求める逆運動計算をまとめる。

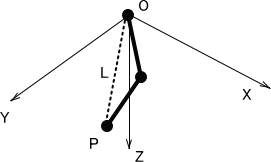
原点Oと肉球点P間の距離Lは

J3はLと腕の長さlより

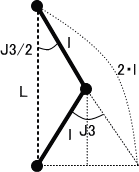
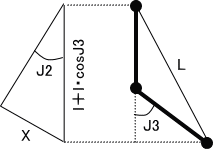
J2は座標xがJ2とJ3により決定することから、

を変形し、

J1を求めるにはJ2・J3からJ1をゼロとし、Pをyz平面に投影した時のY軸値ｙ0及びZ軸値z0を求める。

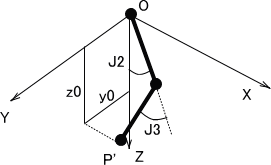
これにJ1による回転を行なった時の座標変換を行なう。

より、

これに先ほどのy0、z0を代入して整理すると、

が得られる。

J1は

となる。

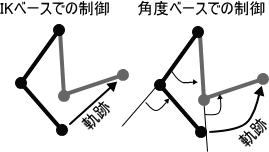
モーション間の補完方法

モーション再生はある関節状態からある関節状態への移行を連続して行なうことによるが、その補完方法によって再生時の動きが異なる。

OPEN-R　SDKに含まれるサンプルプログラム「MoNet」ではキーフレームとして各関節の角度を持ち、角度をリニアに移行させることで補完している。
この場合、目標位置までの肉球点の軌跡は曲線を描くことになり、例えば肉球部を直線移動させるには適度な間隔で直線軌道に目標位置をおき、その間を曲線軌跡で移動することになる。これだと多くのキーフレームが必要となる。また、任意の軌道を取らせたい場合にはいちいち角度に置き換えた状態を作る必要があるので煩雑になる。

ロボット工学的な制御を考えると目標位置指示及び補完計算を座標ベースで行なうことで、歩行などの制御を簡略化させることができる。設計者が考え易くなる分、アイボでの計算量が増えるが十分に短い時間で計算することができるため問題では無いと思われる。

キーフレーム間を座標で補完した時の問題として、移動途中に移行不能な座標を経由する場合が考えられる。角度ベースでの制御であれば目標位置が移動可能であれば補完フレームすべてが移動可能であることが保障される。これらのことを考慮するとダンスなど任意のポーズをとる場合の再生方法は角度ベースでの制御が適しているといえよう。

補完計算の実際

現在の肉球位置を

目標の肉球位置を

とする。

肉球部のフレームあたりの移動距離をとした時、

現在位置から目標位置までの移動距離は

目標位置までの必要フレーム数は

となる。

１フレームあたりの各軸の移動量は

補完フレームの肉球位置は

これに逆運動計算を行い各関節角度とする。

以上