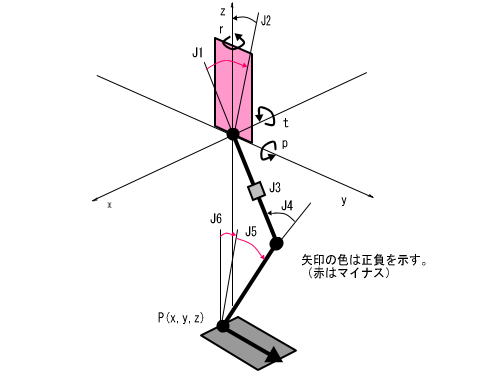
 脚構造を右図のように考え、股関節を原点とした時の足首座標Pを(x,y,z)で表し、股関節の姿勢(胴体の姿勢をチルト角t、ピッチ角p、ロール角rで表した状態を考える。
脚構造を右図のように考え、股関節を原点とした時の足首座標Pを(x,y,z)で表し、股関節の姿勢(胴体の姿勢をチルト角t、ピッチ角p、ロール角rで表した状態を考える。ラムダの逆運動計算(脚編)
2005.5.26
2005.7.23修正
2006.5.3修正
 脚構造を右図のように考え、股関節を原点とした時の足首座標Pを(x,y,z)で表し、股関節の姿勢(胴体の姿勢をチルト角t、ピッチ角p、ロール角rで表した状態を考える。
脚構造を右図のように考え、股関節を原点とした時の足首座標Pを(x,y,z)で表し、股関節の姿勢(胴体の姿勢をチルト角t、ピッチ角p、ロール角rで表した状態を考える。
右図の股関節姿勢(胴体姿勢)は正立しているが、t,p,rが0以外の時は右図の座標はそれぞれの角度回転した形となる。J1及びJ2は直交座標x-y-zからの角度のように描かれているが、実際には股関節姿勢角度分回転した座標との角度となるので注意が必要である。
<足首座標の逆運動学計算>
原点oから足首座標pの距離は
となる。
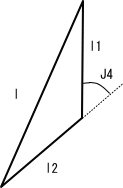 股関節から膝まで、膝から足首までの長さをそれぞれl1,l2としたとき、余弦定理より
股関節から膝まで、膝から足首までの長さをそれぞれl1,l2としたとき、余弦定理より
これを整理し
となる。
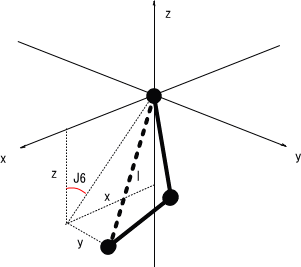 J6関節について考える。J6は、左図のように表せる。
J6関節について考える。J6は、左図のように表せる。
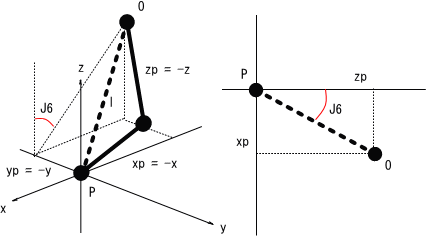 これは右図のように書き直すことができる。
これは右図のように書き直すことができる。
これより、J6は下の式によって表すことができる。
となる。
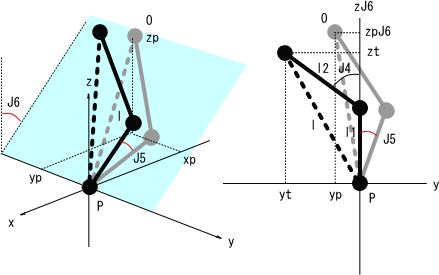 次にy軸周りにJ6回転した座標における、J5=0の時を考える。
次にy軸周りにJ6回転した座標における、J5=0の時を考える。
![]()
![]()
となる。ここで、J4の関節構造より、ytはマイナスとなる。
これをx軸周りにJ5回転すると、
![]()
これを整理して、
ただし、
(ここで、sign(zp)はzp>=0の時、1を、zp<0の時-1を返す関数)
また、xp = -x, yp = -y, zp = -z
以上で、J4,J5,J6による、股関節を原点としたときの足首座標の逆運動計算が完了する。
<股関節姿勢の逆運動学計算>
次に、股関節姿勢の算出を行う。
足首座標が決定した状態での股関節姿勢はJ1,J2,J3によって決定される。
以下の記述では回転行列による座標変換をRot(axis,angle)にて表す。
Rot(x,t)の場合、x軸周りにt(rad)の座標回転変換を行うことを示す。
また、sin(p)をsp, cos(J1)をc1というふうに表す。
股関節の姿勢をJ1からJ6であらわすと
r654321 = Rot(y,J6)・Rot(x,J5)・Rot(y,J4)・Rot(z,J3)・Rot(x,J2)・Rot(y,J1)
一方股関節の姿勢は
rrpt = Rot(z,r)・Rot(y,p)・Rot(x,t)
r654321 = rrpt
なので、
Rot(y,-J4)・Rot(x,-J5)・Rot(y,-J6)・r654321 = Rot(y,-J4)・Rot(x,-J5)・Rot(y,-J6)・rrpt
すなわち、
Rot(z,J3)・Rot(x,J2)・Rot(y,J1) = Rot(y,-J4)・Rot(x,-J5)・Rot(y,-J6)・Rot(z,r)・Rot(y,p)・Rot(x,t)
行列に展開すると、
と置く。
rrpt = crcp -srct+crspst srst+crspct = a11 a12 a13 srcp crct+srspst -crst+srspct a21 a22 a23 -sp cpst cpct a31 a32 a33
r321 = c3c1-s3s2s1 -s3c2 c3s1+s3s2c1 s3c1+c3s2s1 c3c2 s3s1-c3s2c1 -c2s1 s2 c2c1 r_4_5_6rpt= c6a11-s6a31 c6a12-s6a32 c6a13-s6a33 c4s5s6a11+s4c5s6a11
+c4c5a21-s4s5a21
+c4s5c6a31+s4c5c6a31c4s5s6a12+s4c5s6a12
+c4c5a22-s4s5a22
+c4s5c6a32+s4c5c6a32c4s5s6a13+s4c5s6a13
+c4c5a23-s4s5a23
+c4s5c6a33+s4c5c6a33-s4s5s6a11+c4c5s6a11
-s4c5a21-c4s5a21
-s4s5c6a31+c4c5c6a31-s4s5s6a12+c4c5s6a12
-s4c5a22-c4s5a22
-s4s5c6a32+c4c5c6a32-s4s5s6a13+c4c5s6a13
-s4c5a23-c4s5a23
-s4s5c6a33+c4c5c6a33
これより整理して、
-c2s1 -s4s5s6a11+c4c5s6a11-s4c5a21-c4s5a21-s4s5c6a31+c4c5c6a31 tan(J1) = - ----------- = - ---------------------------------------------------------- c2c1 -s4s5s6a13+c4c5s6a13-s4c5a23-c4s5a23-s4s5c6a33+c4c5c6a33
-s3c2 c6a12-s6a32 tan(J3) = - ------- = - -------------------------------------------------------------- c3c2 c4s5s6a12+s4c5s6a12+c4c5a22-s4s5a22+c4s5c6a32+s4c5c6a32
s2 s2 -s4s5s6a12+c4c5s6a12-s4c5a22-c4s5a22-s4s5c6a32+c4c5c6a32 tan(J2) = ------------------ = ---- = ------------------------------------------------------------------- c3*(c3c2) -s3*(-s3c2) c2 c3 * ( c4s5s6a12+s4c5s6a12+c4c5a22-s4s5a22+c4s5c6a32+s4c5c6a32 )
-s3 * ( c6a12-s6a32 )